Pistas para reconstruir el atropello de un turismo a un peatón adulto
Uno de los recursos más utilizados por el perito en la reconstrucción de accidentes de tráfico, y más concretamente en la reconstrucción de atropellos, es el cálculo de la velocidad de atropello en función de la proyección del peatón. En este artículo daremos pistas de cómo hacer un cálculo rápido, pero aproximado, de la velocidad que llevaba el vehículo en el instante del atropello. Nos centraremos en atropellos de vehículos turismo a peatones adultos, que son los que comprenden el mayor porcentaje de atropellos.
Determinar el punto de atropello
Lo primera que tendremos que determinar, con la mayor precisión posible, es el punto donde se produce el atropello. Unos de los datos que normalmente se recoge en el atestado policial es la posición final del peatón tras el atropello, pero es más complicado, en estos casos, debido a la ausencia de vestigios que lo determinen, el punto donde se produce el atropello. En este caso deberemos referirnos a las declaraciones de los testigos, la procedencia o destino del peatón, huellas o vestigios dejados por el peatón o los vehículos, etc. Una vez determinado el posible punto de atropello, mediremos la distancia recorrida por el peatón hasta su posición final en su movimiento de proyección tras el atropello. Esta distancia es una información valiosa para determinar la velocidad del vehículo en el instante del atropello.
Método de Searle
Existen numerosos autores que nos proporcionan diversos métodos y formulas para el cálculo de la velocidad en función de la distancia de proyección. El más extendido y más conocido es John A. Searle.
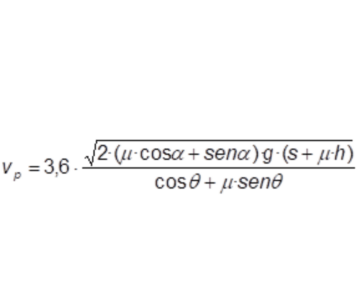
Para determinar la velocidad del vehículo en el momento del atropello más probable, Searle indica que se debe incrementar el valor mínimo de la velocidad de proyección obtenida considerando la eficiencia de la proyección, que depende de la forma del frontal del vehículo en relación con la altura del peatón, y de si el vehículo se hallaba ya frenando o no en el momento del atropello. El autor del estudio, John A. Searle, fija este factor corrector en un 20% aproximadamente (SAE PAPER 930659. John A. Searle. “The Physics of Throw Distance in Accident Reconstruction”.) La expresión que nos da el valor mínimo es la siguiente:
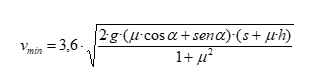
Esta expresión la podemos simplificar si consideramos que el terreno es plano, quedando del siguiente modo:
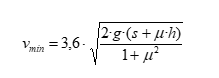
:
Searle también establece el valor del coeficiente de rozamiento del peatón con el asfalto en µ =0,7. Considerando el valor de la constante gravitatoria g=9,81m/s2, y el de h≈1metro (diferencia del centro de gravedad del peatón antes y después del atropello), la expresión se puede simplificar en:
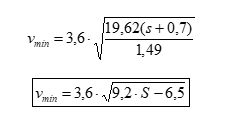
Donde S es la distancia de proyección del peatón en metros.
A este resultado le sumaremos el 20% establecido anteriormente, obteniendo un valor que nos dará una primera idea aproximada de la velocidad del vehículo en el atropello.
Con este sencillo cálculo podremos evaluar de manera rápida si el caso que tenemos entre manos tiene defensa o no en cuanto a un posible exceso de velocidad del vehículo que atropella.
Jordi Rivera García
Perito principal en Ipsum Reconstrucción de accidentes de tráfico




