INTRODUCCIÓN
Existen diferentes métodos que utilizamos los peritos para calcular la velocidad a la que circulaba un vehículo cuando se produce un accidente de tráfico. Sin embargo, generalizando, podemos afirmar que la mayoría de métodos de cálculo parten de uno de estos dos principios físicos que vamos a abordar en este post: el principio de conservación de la energía y el principio de conservación de la cantidad de movimiento.
PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA
Como, posiblemente, algunos de vosotros recordéis de vuestra época de estudiantes de secundaria, este principio parte de afirmar que “la energía ni se crea ni se destruye, sino que se transforma”. Por lo tanto, aplicando este principio físico a la reconstrucción de un siniestro vial, podemos afirmar que la energía que aporta uno o varios objetos en movimiento ha de ser igual a la energía transformada durante su proceso de detención.
Esta energía que aporta un cuerpo por el hecho de estar en movimiento es la que se denomina en física energía cinética, que se suele expresar mediante la siguiente fórmula:
Donde:
- Ec: Es la energía cinética del cuerpo en movimiento (expresada en julios)
- m: es la masa del cuerpo en movimiento (expresada en kilogramos)
- v: es el valor de la velocidad del cuerpo en movimiento (expresada en metros por segundo).
Esto nos lleva a afirmar, cuando reconstruimos un accidente de tráfico, que la suma de las energías cinéticas previas a una colisión ha de ser igual a la suma de las energías transformadas durante el proceso de detención de los vehículos implicados. De lo que se trata, por tanto, es de saber qué energías transformadas existían antes y después del siniestro vial analizado, para construir una ecuación basada en el principio de conservación de la energía que nos permitirá aislar y conocer la velocidad de los vehículos implicados.
¿Cómo lo haremos? Lo que haremos será calcular de forma individualizada cada una de las energías transformadas, para luego sumarlas y descubrir la cantidad total de energía disipada.
Principales problemas que podemos encontrar a la hora de determinar la velocidad partiendo del principio físico de conservación de la energía
¿Qué pasa con este método cuando en un incidente vial existen dos cuerpos en movimiento?
A no ser que conozcamos la velocidad de uno de estos cuerpos, construir la ecuación antes descrita nos llevará a obtener una ecuación de primer grado con dos incógnitas (la velocidad del vehículo A y la velocidad del vehículo B, que, en consecuencia, no podremos resolver).
Sin embargo, no tendremos problemas para utilizar este método cuando:
– un solo vehículo esté en movimiento y el otro se encuentre parado. En estos casos existe una única energía cinética previa, la del vehículo que estaba en movimiento.
-uno de los vehículos implicados llevase tacógrafo, el cual nos daría ya el dato de la velocidad.
-se tratase de un atropello a un peatón. En estos casos, podríamos obtener la velocidad del peatón realizando pruebas con personas de edades y características físicas similares a las del peatón atropellado; o bien podríamos partir de tablas estadísticas que nos proporcionarían velocidades bastante aproximadas
¿Cómo entenderlo a partir de un ejemplo práctico?
Pongamos el siguiente supuesto: se produce un alcance del turismo A al turismo B, mientras B está parado. Para calcular la velocidad del turismo A, partimos de:
ECA + ECB= EDA + EDB + E’CA + E’CB
Donde:
ECA es la energía cinética del turismo A
ECB es la energía cinética del turismo B, en este caso, 0
EDA es la energía de deformación del turismo A
EDB es la energía de deformación del turismo B
E’CA es la energía cinética poscolisión del turismo A
E’CB es la energía cinética poscolisión del turismo B
Como ECB 0, podemos simplificar la igualdad ECA = EDA + EDB + E’CA + E’CB
Sabemos que ECA =1/2MAVA2, si lo que queremos aislar es la velocidad, diremos que:
¿Cómo utilizar el principio de conservación de la energía para calcular la velocidad cuando dos cuerpos están en movimiento?
Como hemos dicho anteriormente, la mayoría de veces no podremos partir del principio de conservación de la energía para determinar la velocidad de 2 cuerpos en movimiento de velocidad desconocida, en tanto que obtendríamos una ecuación de primer grado con 2 incógnitas (velocidad de A y velocidad de B, que no podríamos resolver). Sin embargo, existe una excepción que sí nos permitiría hacerlo: se trata de aquellos casos en los que uno de los vehículos accede a una intersección o a un giro muy cerrado desde la posición de parado. En estos casos, si conocemos la máxima aceleración que puede alcanzar el vehículo y conocemos la distancia que media desde su posición de salida hasta el punto de colisión, podremos calcular la velocidad máxima que dicho vehículo pudo alcanzar en el punto de colisión y hacer una estimación en base a este dato. Resolviendo la velocidad de este vehículo, volveríamos, pues, a tener una ecuación de una sola incógnita.
¿Cuáles son las energías que pueden intervenir en una colisión y cómo calcularlas para poder aislar y hallar la velocidad basándonos en el principio de conservación de la energía?
La energía cinética :
ya hemos dicho que es aquella que posee un cuerpo por el hecho de moverse.
La energía de rozamiento:
es aquella que se genera a partir de la fricción de diferentes superficies en contacto. Se trata de una de las energías que aglutina un mayor porcentaje de energía transformada en un accidente de tráfico.
La energía de rozamiento (Eroz) es igual a la fuerza de rozamiento (FROZ) multiplicada por la distancia recorrida por el cuerpo en movimiento (D).
Donde:
- M es la masa del vehículo implicado
- G es la constante gravitatoria
- µ es el coeficiente de adherencia
- D es la distancia recorrida por el vehículo o cuerpo en movimiento
Además, a la hora de calcular la energía de rozamiento, será importante tener en cuenta en nuestra reconstrucción la inclinación de la carretera en la que se produjo el siniestro vial. Así, cuando el tramo en el que se haya producido la dinámica de rozamiento tuviese inclinación ascendente o descendente, se ha de calcular la energía de rozamiento a partir de la siguiente fórmula:
Eroz= MG·(µ ±p)·D
Donde p es la pendiente expresada en tanto por uno, la sumaremos a µ si es positiva y la restaremos a µ si es negativa. Así, si la pendiente fuese positiva de un 5% la fórmula quedaría:
Eroz= MG·(µ +5)·D
Esta fórmula no es aplicable para pendientes mayores a 20°, las cuales son muy poco frecuentes en la reconstrucción de siniestros viales.
La energía transformada en el caso de giro de un vehículo:
En la investigación de un siniestro vial podemos encontrar que los vehículos que colisionan realizan movimientos circulares. Esto sucede cuando las fuerzas que se aplican sobre un vehículo no pasan por su centro de gravedad (se trata de fuerzas excéntricas que producen sobre el vehículo un momento angular o momentum), por lo que será necesario transformar la energía cinética portada inicialmente en la energía de rozamiento que resulta de este giro.
Para calcular la energía del giro podemos aplicar la siguiente fórmula:
Eroz= MG·µ ·α·r
Donde α es el ángulo de giro del vehículo en radianes y r es el radio de giro (el cual se ha de calcular de forma específica en función de cómo sea el giro).
La energía potencial gravitatoria:
Se trata de un tipo de energía asociada a la posición que tienen los cuerpos (no a su movimiento), es la energía que posee un cuerpo por el hecho de hallarse bajo la acción de la gravedad. En la reconstrucción de accidentes de tráfico solo la utilizaremos en el caso de que intervenga en el siniestro un cuerpo en movimiento ascendiendo sobre un plano inclinado. En este caso, la gravedad realizará un trabajo negativo sobre el vehículo que asciende y la energía potencial será una de las energías en las que se transformará la energía cinética del vehículo hasta llegar a detenerse.
En cambio, cuando el cuerpo en movimiento implicado en un siniestro vial descienda, la energía potencial se transformará en energía cinética.
Para calcular la energía potencial gravitatoria de los vehículos implicados, partiríamos de la siguiente fórmula:
Ep=m⋅g⋅h
Donde:
- Ep es la energía potencial del cuerpo expresada en Julios
- m es la masa del cuerpo expresada en Kilogramos
- g es el valor de la aceleración que provoca la gravedad expresada en metros por segundo al cuadrado
- h es la altura a la que se encuentra el cuerpo expresada en metros
La energía transformada en un movimiento parabólico:
Hablamos de movimiento parabólico para referirnos a una composición de movimientos en dos dimensiones: un movimiento rectilíneo uniforme en el eje horizontal y un movimiento rectilíneo uniformemente retardado en el eje vertical. Un ejemplo de este tipo de movimiento lo encontraríamos en el cuerpo de un motorista, que sale proyectado después de impactar con un turismo.
Para calcular esta energía, será necesario calcular primero la velocidad de salida del objeto proyectado, la cual se puede obtener partiendo de la siguiente fórmula:
Donde:
- G es la constante gravitatoria
- X es la distancia recorrida en la parábola del móvil
- α es el ángulo de salida del móvil con relación al plano horizontal
Así, una vez conocida la velocidad y la masa del objeto, podremos calcular la energía cinética inicial del objeto. Aplicando la fórmula de la energía cinética y sustituyendo los valores correspondientes del cuerpo en movimiento y su velocidad de salida, obtendremos la energía disipada en el movimiento parabólico.
Energía de velocidad perdida en la actuación del sistema de frenado:
Desde que se inicia una acción de frenada hasta que se activa el bloqueo efectivo de las ruedas existe un tiempo de actuación del sistema, que oscila entre los 0,2 y 0,6 segundos. Durante este lapso de tiempo se genera una energía disipada a causa de la fricción de los mecanismos de freno. Para calcularla, partimos de la siguiente fórmula:
Donde:
- Vf es la velocidad final
- Vi es la velocidad inicial
- α es la deceleración media
- t es el tiempo de actuación del sistema
Energía transformada en la deformación:
Si partimos del principio de conservación de la energía, podemos afirmar que el trabajo necesario para producir determinados daños o deformaciones en un siniestro vial ha de ser igual a la energía cinética portada por el móvil que produce la deformación. A partir de esta afirmación, si logramos conocer la energía desarrollada por el móvil que produce las deformaciones, podremos conocer la velocidad a la que este vehículo impactó para que se produjesen los daños.
Para realizar este tipo de cálculos necesitamos disponer de otro dato muy importante, que es coeficiente de rigidez del vehículo, un indicador variable que depende del tipo de vehículo y de la zona del vehículo en la que se impacta.
Existen diferentes fórmulas y métodos para calcular la energía de deformación, siendo los más conocidos los de Campbell y Mc Henry.
La expresión más sencilla de estas fórmulas de cálculo de la energía de deformación es:
d= ½ KCX²
Donde:
- d es la energía de deformación
- K es el Coeficiente rigidez
- C es el Coeficiente de participación de la zona afectada
- X es la Profundidad media
Uno de los autores más citados para calcular la energía de deformación fue Mc Henry y su programa Crash3, un programa con un rango de certidumbre de aproximadamente un 12%, basado en las postulaciones de Campbell y cuya utilidad es estimar la energía absorbida como trabajo de deformación permanente en un choque.
Sin entrar más allá en cálculos que pueden ser difíciles de entender en este post, mencionaremos la igualdad:
F= A+ B · D
Donde:
- F es la fuerza de Deformación
- A es el coeficiente de deformación elástica
- B es el coeficiente de rigidez.
- D es la profundidad de la deformación
Se trata de un método que sería válido para calcular la energía de deformación en colisiones frontales o laterales con amplias áreas afectadas, pero no en el resto de casos.
PRINCIPIO DE CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO
Este método de cálculo parte de la premisa que la cantidad de movimiento existente antes de una colisión en un siniestro vial ha de ser igual a la cantidad de movimiento existente tras la misma. Para realizar cálculos sirviéndonos de este principio físico, el perito reconstructor sitúa el origen de los cálculos en el punto de colisión.
En estos casos, los peritos reconstructores acostumbramos a tomar como punto de partida un croquis del accidente. En este croquis plasmamos de manera gráfica y exacta la dinámica seguida por cada una de las unidades implicadas en el siniestro: el punto de impacto y las posiciones finales de cada uno de los cuerpos en movimiento. Sobre el croquis situamos, además, el sistema inercial de referencia, como punto de partida para estudiar los desplazamientos de cada una de las unidades implicadas.
Así:
- Crearemos un eje de coordenadas cartesianas y en el punto 0 quedará ubicado en el punto de colisión.
- Una vez hayamos establecido sobre el croquis nuestro eje de coordenadas cartesianas, ubicaremos en él los vectores de la cantidad de movimiento de cada uno de los móviles existentes antes y después de la colisión.
- Concretaremos los ángulos que cada uno de los vectores cantidad de movimiento forman sobre el eje de abscisas y calcularemos sus razones trigonométricas (únicamente seno y coseno).
- Calcularemos las velocidades de salida o poscolisión de cada una de las unidades participantes.
- Descompondremos cada uno de los vectores pre y poscolisión en sus correspondientes componentes sobre el eje de abscisas, obteniendo una ecuación lineal de primer grado con 2 incógnitas
- Descompondremos otra vez cada uno de los vectores pre y poscolisión en sus correspondientes componentes sobre el eje de ordenadas, obteniendo de nuevo una ecuación lineal de primer grado con 2 incógnitas.
- Con ambas igualdades plantearemos un sistema de 2 ecuaciones con 2 incógnitas, que podemos resolver
Para hacer todo esto, el cálculo de velocidad de salida de la colisión de cada uno de los vehículos implicados en el impacto lo entenderemos como un cálculo concreto y particular dentro de la reconstrucción global del accidente, al que llegaremos partiendo del método descrito en el punto anterior, basándonos en el principio de conservación de la energía. Una vez tengamos la velocidad de salida de cada uno de los móviles implicados en la colisión, podremos basarnos en el principio de conservación del movimiento, que resolveremos a través de un método vectorial.
Cálculo de la velocidad en embestidas frontolaterales:
En colisiones con ángulos de entrada de 0° y 90° no va a ser necesario plantear un sistema de ecuaciones con 2 incógnitas, porque sobre cada eje vamos a poder despejar ya una incógnita. Se trata de un cálculo de la velocidad de los más fáciles, pues al descomponer los vectores cantidad de movimiento sobre cada uno de los ejes de coordenadas se obtendrá una ecuación lineal con una única incógnita. Así, podremos resolver la velocidad de los 2 móviles resolviendo ambas ecuaciones.
Cálculo de la velocidad en colisiones en ángulos diferentes a 90°:
La metodología será la misma que hemos descrito en el apartado anterior, pero en este caso obtendremos 2 ecuaciones con 2 incógnitas que podremos despejar resolviendo el sistema de ecuaciones.
Algunos problemas recurrentes al aplicar el principio de conservación de la cantidad de movimiento para hallar la velocidad de los vehículos implicados en el siniestro:
A la hora de realizar un cálculo vectorial, podemos encontrarnos con que la masa de los vehículos implicados en una colisión varía, bien porque tras la colisión ambos vehículos se mueven unidos formando un único bloque, bien porque uno de los vehículos divide su masa tras el impacto (una colisión con una moto en la que, tras el impacto, motorista y motocicleta se separan). En el primer caso, cuando dos vehículos forman un único bloque tras el impacto, lo que haremos será servirnos de un único sumando para el vector cantidad de movimiento poscolisión en cada una de las ecuaciones. En el segundo caso, cuando la masa de uno de los móviles se divide, lo que haremos será servirnos de 3 sumandos, de 3 vectores cantidad de movimiento poscolisión.
Otro problema con el que podemos encontrarnos al descomponer cada uno de los vectores cantidad de movimiento para obtener nuestro sistema de ecuaciones, es que los vehículos implicados desarrollen su dinámica accidental sobre un mismo eje. Esto puede producirse en supuestos de alcances dinámicos o colisiones frontales entre 2 vehículos. nos encontraremos que lo que obtendremos es una ecuación lineal con 2 incógnitas (las velocidades de ambos vehículos). Para poder resolver este problema formularemos una nueva ecuación aplicando el coeficiente de restitución, el cual está directamente relacionado con el tipo de choque desarrollado por los vehículos implicados en una colisión. Este coeficiente expresa la pérdida o no de energía cinética entre 2 cuerpos que colisionan, según las fuerzas de restitución y la elasticidad de los materiales. Sin entrar en más detalles aquí, podemos afirmar que, grosso modo, el coeficiente de restitución en la reconstrucción de accidentes de tráfico suele oscilar entre 0,2 y 0.
FUENTES BIBLIOGRÁFICAS CONSULTADAS Y/O RECOMENDADAS
CAMPBELL, K: Energy basis for collision severity
FISICALAB: https://www.fisicalab.com/ (sitio web de consulta general de conceptos)
MCHENRY, R: A comparison of results obtained with different analytical techniques for reconstruction of highway accidents
Ainhoa M. Muguruza


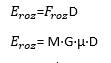
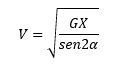



9 comentarios
Felicitaciones por el articulo
Saludos desde Buenos Aires
Mussino
¡Muchas gracias! Saludos
muchas gracias Saludos desde coatzacoalcos Veracruz mexico bendiciones
Gracias a ti por leernos.
¡Un abrazo!
Agradecimiento y saludos desde LIMA-PERU…estamos en la misma línea de trabajo..Dios lo bendiga…
Muy buena información, gracias..
Mis felicitaciones por su aportación científica.
¡Gracias a ti por leernos, Hector!
Buenas noches, le pido su ayuda para determinar la velocidad de un vehículo que se salio de carretera, no frenó, y quedó a 80 metros del punto donde se salió, paralelo a la carretera, dió unas cinco vueltas de costado.
Muy bueno el artículo. Muchas gracias por la información. Saludos cordiales desde Río Gallegos Provincia de Santa Cruz Argentina.