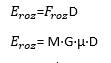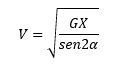INTRODUCCIÓ
Hi ha diferents mètodes que utilitzem els pèrits per calcular la velocitat a la qual circulava un vehicle quan es produeix un accident de trànsit. No obstant això, generalitzant, podem afirmar que la majoria de mètodes de càlcul parteixen d’un dels dos principis físics que abordarem en aquest post: el principi de conservació de l’energia i el principi de conservació de la quantitat de moviment.
PRINCIPI DE CONSERVACIÓ DE L’ ENERGÍA
Com, possiblement, alguns de vosaltres recordeu de la vostra època d’estudiants de secundària, aquest principi parteix d’afirmar que “l’energia ni es crea ni es destrueix, sinó que es transforma”. Per tant, aplicant aquest principi físic a la reconstrucció d’un sinistre viari, podem afirmar que l’energia que aporta un o diversos objectes en moviment ha de ser igual a l’energia transformada durant el seu procés de detenció.
Aquesta energia que aporta un cos pel fet d’estar en moviment és la que s’anomena a física energía cinètica, que se sol expressar mitjançant la següent fórmula:
On:
- Ec: és l’energia cinètica del cos en moviment (expressada en joules)
- m: és la masa del cos en moviment (expressada en kilograms)
- v: és el valor de la velocitat del cos en moviment (expressada en metres per segon).
Això ens porta a afirmar, quan reconstruïm un accident de trànsit, que la suma de les energies cinètiques prèvies a una col·lisió ha de ser igual a la suma de les energies transformades durant el procés de detenció dels vehicles implicats. Del que es tracta, per tant, és de saber quines energies transformades existien abans i després del sinistre viari analitzat, per construir una equació basada en el principi de conservació de l’energia que ens permetrà aïllar i conèixer la velocitat dels vehicles implicats.
Com ho farem? El que farem serà calcular de forma individualitzada cadascuna de les energies transformades, per després sumar-les i descobrir la quantitat total d’energia dissipada.
Principals problemes que podem trobar a l’hora de determinar la velocitat partint del principi físic de conservació de l’energia
Què passa amb aquest mètode quan en un incident viari hi ha dos cossos en moviment?
A no ser que coneguem la velocitat d’un d’aquests cossos, construir l’equació abans descrita ens portarà a obtenir una equació de primer grau amb dues incògnites (la velocitat del vehicle A i la velocitat del vehicle B, que, en conseqüència, no podrem resoldre).
No obstant això, no tindrem problemes per utilitzar aquest mètode quan:
-un sol vehicle estigui en moviment i l’altre es trobi aturat. En aquests casos hi ha una única energia cinètica prèvia, la del vehicle que estava en moviment.
-un dels vehicles implicats portés tacògraf, el qual ens donaria ja la dada de la velocitat.
-es tractés d’un atropellament a un vianant. En aquests casos, podríem obtenir la velocitat del vianant realitzant proves amb persones d’edats i característiques físiques similars a les del vianant atropellat; o bé podríem partir de taules estadístiques que ens proporcionarien velocitats bastant aproximades.
Com entendre-ho a partir d’un exemple pràctic?
Posem el següent supòsit: es produeix un encalç del turisme A al turisme B, mentre B està aturat. Per calcular la velocitat del turisme A, partim de:
ECA + ECB= EDA + EDB + E’CA + E’CB
On:
ECA és l’energia cinètica del turisme A
ECB és l’energia cinètica del turismeB, en aquest cas 0
EDA és l’energia de deformació del turisme A
EDB és l’energia de deformació del turisme B
E’CA és l’energia cinètica postcolisió del turisme A
E’CB és l’energia cinètica postcolisió del turisme B
Com ECB és 0, podem simplificar la igualtat ECA = EDA + EDB + E’CA + E’CB
Sabem que ECA =1/2MAVA2, si el que volem aïllar és la velocitat, direm que:
Com utilitzar el principi de conservació de l’energia per calcular la velocitat quan dos cossos estan en moviment?
Com hem dit anteriorment, la majoria de vegades no podrem partir del principi de conservació de l’energia per a determinar la velocitat de 2 cossos en moviment de velocitat desconeguda, en tant que obtindríem una equació de primer grau amb 2 incògnites (velocitat de A i velocitat de B, que no podríem resoldre). No obstant això, hi ha una excepció que sí que ens permetria fer-ho: es tracta d’aquells casos en què un dels vehicles accedeix a una intersecció o a un gir molt tancat des de la posició d’ aturat. En aquests casos, si coneixem la màxima acceleració a què pot arribar el vehicle i coneixem la distància que hi ha des de la seva posició de sortida fins al punt de col·lisió, podrem calcular la velocitat màxima que el vehicle va poder assolir en el punt de col·lisió i fer una estimació basant-nos en aquesta dada. Resolent la velocitat d’aquest vehicle, tornaríem, doncs, a tenir una equació d’una sola incògnita.
Quines són les energies que poden intervenir en una col·lisió i com calcular-les per poder aïllar i trobar la velocitat basant-nos en el principi de conservació de l’energia?
L’ energia cinètica :
ja hem dit que és aquella que posseeix un cos pel fet de moure’s.
L’ energia de fregament:
és aquella que es genera a partir de la fricció de diferents superfícies en contacte. Es tracta d’una de les energies que aglutina un major percentatge d’energia transformada en un accident de trànsit.
L’energia de fregament (Eroz) és igual a la força de fregament(FROZ) multiplicada per la distància recorreguda pel cos en moviment (D).
On:
- M és la massa de el vehicle implicat
- G és la constant gravitatòria
- μ és el coeficient d’adherència
- D és la distància recorreguda pel vehicle o cos en moviment
A més, a l’hora de calcular l’energia de fregament, serà important tenir en compte en la nostra reconstrucció la inclinació de la carretera en la qual es va produir el sinistre viari. Així, quan el tram en què s’hagi produït la dinàmica de fregament tingués inclinació ascendent o descendent, s’ha de calcular l’energia de fregament a partir de la següent fórmula:
Eroz= MG·(µ ±p)·D
On p és el pendent expressat en tant per un, el sumarem a μ si és positiu i el restarem a μ si és negatiu. Així, si el pendent és positiu d’un 5%, la fórmula quedaria:
Eroz= MG·(µ +5)·D
Aquesta fórmula no és aplicable per pendents majors a 20 °, les quals són molt poc freqüents en la reconstrucció de sinistres viaris.
L’energia transformada en el cas de gir d’un vehicle:
En la investigació d’un sinistre viari podem trobar que els vehicles que xoquen realitzen moviments circulars. Això succeeix quan les forces que s’apliquen sobre un vehicle no passen pel seu centre de gravetat (es tracta de forces excèntriques que produeixen sobre el vehicle un moment angular o momentum), pel que serà necessari transformar l’energia cinètica portada inicialment en l’energia de fregament que resulta d’aquest gir.
Per calcular l’energia del gir podem aplicar la fórmula següent:
Eroz= MG·µ ·α·r
On α és l’angle de gir del vehicle en radiants i r és el radi de gir (el qual s’ha de calcular de forma específica en funció de com sigui el gir).
L’ energia potencial gravitatòria:
Es tracta d’un tipus d’energia associada a la posició que tenen els cossos (no al seu moviment), és l’energia que posseeix un cos pel fet de trobar-se sota l’acció de la gravetat. En la reconstrucció d’accidents de trànsit només la utilitzarem en el cas que intervingui en el sinistre un cos en moviment ascendint sobre un pla inclinat. En aquest cas, la gravetat realitzarà un treball negatiu sobre el vehicle que ascendeix i l’energia potencial serà una de les energies en què es transformarà l’energia cinètica del vehicle fins a arribar a aturar-se.
En canvi, quan el cos en moviment implicat en un sinistre viari descendeixi, l’energia potencial es transformarà en energia cinètica.
Per calcular l’energia potencial gravitatòria dels vehicles implicats, partiríem de la següent fórmula:
Ep=m⋅g⋅h
On:
- Ep és l’energia potencial del cos expressada en Joules
- m és la massa de el cos expressada en quilograms
- g és el valor de l’acceleració que provoca la gravetat expressada en metres per segon al quadrat
- h és l’altura a la qual es troba el cos expressada en metres
L’energia transformada en un moviment parabòlic:
Parlem de moviment parabòlic per referir-nos a una composició de moviments en dues dimensions: un moviment rectilini uniforme en l’eix horitzontal i un moviment rectilini uniformement retardat en l’eix vertical. Un exemple d’aquest tipus de moviment el trobaríem en el cos d’un motorista, que surt projectat després d’impactar amb un turisme.
Per calcular aquesta energia, serà necessari calcular primer la velocitat de sortida de l’objecte projectat, la qual es pot obtenir partint de la següent fórmula:
On:
- G és la constant gravitatòria
- X és la distància recorreguda en la paràbola del mòbil
- α és l’angle de sortida del mòbil amb relació al pla horitzontal
Així, un cop coneguda la velocitat i la massa de l’objecte, podrem calcular l’energia cinètica inicial de l’objecte. Aplicant la fórmula de l’energia cinètica i substituint els valors corresponents del cos en moviment i la seva velocitat de sortida, obtindrem l’energia dissipada en el moviment parabòlic.
Energia de velocitat perduda en l’actuació de sistema de frenada:
Des que s’inicia una acció de frenada fins que s’activa el bloqueig efectiu de les rodes hi ha un temps d’actuació del sistema, que oscil·la entre els 0,2 i 0,6 segons. Durant aquest lapse de temps es genera una energia dissipada a causa de la fricció dels mecanismes de fre. Per calcular-la, partim de la següent fórmula:
On:
- Vf és la velocitat final
- Vi és la velocitat inicial
- α és la desacceleració mitjana
- t és el temps d’actuació de sistema
Energia transformada en la deformació:
Si partim del principi de conservació de l’energia, podem afirmar que el treball necessari per produir determinats danys o deformacions en un sinistre viari ha de ser igual a l’energia cinètica portada pel mòbil que produeix la deformació. A partir d’aquesta afirmació, si aconseguim conèixer l’energia desenvolupada pel mòbil que produeix les deformacions, podrem conèixer la velocitat a la qual aquest vehicle va impactar perquè es produïssin els danys.
Per realitzar aquest tipus de càlculs necessitem disposar d’un altre dada molt important, que és el coeficient de rigidesa del vehicle, un indicador variable que depèn del tipus de vehicle i de la zona del vehicle en què es impacta.
Hi ha diferents fórmules i mètodes per calcular l’energia de deformació, sent els més coneguts els de Campbell i Mc Henry.
L’expressió més senzilla d’aquestes fórmules de càlcul de l’energia de deformació és:
d= ½ KCX²
Donde:
- d és l’energia de deformació
- K és el Coeficient de rigidesa
- C és el Coeficient de participació de la zona afectada
- X és la Profunditat mitjana
Un dels autors més citats per calcular l’energia de deformació va ser Mc Henry i el seu programa Crash3, un programa amb un rang de certesa d’aproximadament un 12%, basat en les postulacions de Campbell i la utilitat del qual és estimar l’energia absorbida com a treball de deformació permanent en un xoc.
Sense aprofundir en càlculs que poden ser difícils d’entendre en aquest post, esmentarem la igualtat:
F= A+ B · D
On:
- F és la força de deformació
- A és el coeficient de deformació elàstica
- B és el coeficient de rigidesa.
- D és la profunditat de la deformació
Es tracta d’un mètode que seria vàlid per a calcular l’energia de deformació en col·lisions frontals o laterals amb àmplies àrees afectades, però no en la resta de casos.
PRINCIPI DE CONSERVACIÓ DE LA QUANTITAT DE MOVIMENT
Aquest mètode de càlcul parteix de la premissa que la quantitat de moviment existent abans d’una col·lisió en un sinistre viari ha de ser igual a la quantitat de moviment existent després de la mateixa. Per realitzar càlculs servint-nos d’aquest principi físic, el perit reconstructor situa l’origen dels càlculs en el punt de col·lisió.
En aquests casos, els perits reconstructors acostumem a prendre com a punt de partida un croquis de l’accident. En aquest croquis plasmem de manera gràfica i exacta la dinàmica seguida per cadascuna de les unitats implicades en el sinistre: el punt d’impacte i les posicions finals de cadascun dels cossos en moviment. Sobre el croquis situem, a més, el sistema inercial de referència, com a punt de partida per a estudiar els desplaçaments de cadascuna de les unitats implicades.
Així:
- Crearem un eix de coordenades cartesianes i en el punt 0 quedarà ubicat en el punt de col·lisió.
- Un cop haguem establert sobre el croquis el nostre eix de coordenades cartesianes, ubicarem en ell els vectors de la quantitat de moviment de cada un dels mòbils existents abans i després de la col·lisió.
- Concretarem els angles que cadascun dels vectors quantitat de moviment formen sobre l’eix d’abscisses i calcularem les seves raons trigonomètriques (únicament sinus i cosinus).
- Calcularem les velocitats de sortida o poscolisió de cadascuna de les unitats participants.
- Descompondrem cadascun dels vectors pre i poscolisió en els seus corresponents components sobre l’eix d’abscisses, obtenint una equació lineal de primer grau amb 2 incògnites
- Descompondrem altra vegada cadascun dels vectors pre i poscolisió en els seus corresponents components sobre l’eix d’ordenades, obtenint de nou una equació lineal de primer grau amb 2 incògnites.
- Amb les dues igualtats plantejarem un sistema de 2 equacions amb 2 incògnites, que podem resoldre.
Per fer tot això, el càlcul de velocitat de sortida de la col·lisió de cadascun dels vehicles implicats en l’impacte ho entendrem com un càlcul concret i particular dins de la reconstrucció global de l’accident, a què arribarem partint del mètode descrit en el punt anterior, basant-nos en el principi de conservació de l’energia. Un cop tinguem la velocitat de sortida de cadascun dels mòbils implicats en la col·lisió, podrem basar-nos en el principi de conservació del moviment, que resoldrem a través d’un mètode vectorial.
Cálcul de la velocitat en envestides frontolaterals:
En col·lisions amb angles d’entrada de 0 ° i 90 ° no serà necessari plantejar un sistema d’equacions amb 2 incògnites, perquè sobre cada eix podrem ja aïllar una incògnita. Es tracta d’un càlcul de la velocitat dels més fàcils, doncs, en descompondre els vectors quantitat de moviment sobre cadascun dels eixos de coordenades, s’obtindrà una equació lineal amb una única incògnita. Així, podrem resoldre la velocitat dels 2 mòbils resolent les dues equacions.
Càlcul de la velocitat en col·lisions en angles diferents a 90°:
La metodologia serà la mateixa que hem descrit en l’apartat anterior, però en aquest cas obtindrem 2 equacions amb 2 incògnites que podrem aclarir resolent el sistema d’equacions.
Alguns problemes recurrents en aplicar el principi de conservació de la quantitat de moviment per a trobar la velocitat dels vehicles implicats en el sinistre:
A l’hora de realitzar un càlcul vectorial, podem trobar-nos que la massa dels vehicles implicats en una col·lisió varia, bé perquè després de la col·lisió els dos vehicles es mouen units formant un únic bloc, bé perquè un dels vehicles divideix la seva massa després del impacte (una col·lisió amb una moto en la qual, després de l’impacte, motorista i motocicleta se separen). En el primer cas, quan dos vehicles formen un únic bloc després de l’impacte, el que farem serà servir-nos d’un únic sumant per al vector quantitat de moviment poscolisió en cadascuna de les equacions. En el segon cas, quan la massa d’un dels mòbils es divideix, el que farem serà servir de 3 sumands, de 3 vectors quantitat de moviment poscolisió.
Un altre problema amb el qual podem trobar-nos en descompondre cadascun dels vectors quantitat de moviment per obtenir el nostre sistema d’equacions, és que els vehicles implicats desenvolupin la seva dinàmica accidental sobre un mateix eix. Això pot produir-se en supòsits d’encalçaments dinàmics o col·lisions frontals entre 2 vehicles. Ens trobarem que el que obtindrem és una equació lineal amb 2 incògnites (les velocitats dels dos vehicles). Per poder resoldre aquest problema formularem una nova equació aplicant el coeficient de restitució, el qual està directament relacionat amb el tipus de xoc desenvolupat pels vehicles implicats en una col·lisió. Aquest coeficient expressa la pèrdua o no d’energia cinètica entre 2 cossos que xoquen, segons les forces de restitució i l’elasticitat dels materials. Sense entrar en més detalls aquí, podem afirmar que, grosso modo, el coeficient de restitució en la reconstrucció d’accidents de trànsit sol oscil·lar entre 0,2 i 0,4.
FONTS BIBLIOGRÀFIQUES CONSULTADES I / O RECOMANADES
CAMPBELL, K: Energy basis for collision severity
FISICALAB: https://www.fisicalab.com/ (lloc web de consulta general de conceptes)
MCHENRY, R: A comparison of results obtained with different analytical techniques for reconstruction of highway accidents
Ainhoa M. Muguruza